Love, and to be Loved.

我愛你，你是自由的。

2016-07-28 | data science

機器學習常用算法梳理

機器學習算法太多了，分類、回歸、聚類、推薦、圖像識別領域等等，要想找到一個合適算法真的不容易，所以在實際應用中，我們一般都是采用啟發式學習方式來實驗。通常最開始我們都會選擇大家普遍認同的算法，諸如SVM，GBDT，Adaboost，現在深度學習很火熱，神經網絡也是一個不錯的選擇。假如你在乎精度（accuracy）的話，最好的方法就是通過交叉驗證（cross-validation）對各個算法一個個地進行測試，進行比較，然後調整參數確保每個算法達到最優解，最後選擇最好的一個。但是如果你只是在尋找一個“足夠好”的算法來解決你的問題，或者這裡有些技巧可以參考，下面來分析下各個算法的優缺點，基於算法的優缺點，更易於我們去選擇它。

偏差&方差

在統計學中，一個模型好壞，是根據偏差(Bias)和方差(Variance)來衡量的，所以我們先來普及一下偏差和方差：

偏差：描述的是預測值（估計值）的期望E’與真實值Y之間的差距。偏差越大，越偏離真實數據。The bias is error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting).
$Bias[\hat{f}(x)] = E[\hat{f}(x)] - f(x)$

方差：描述的是預測值P的變化範圍，離散程度，是預測值的方差，也就是離其期望值E的距離。方差越大，數據的分布越分散。The variance is error from sensitivity to small fluctuations in the training set. High variance can cause overfitting: modeling the random noise in the training data, rather than the intended outputs.
$Var[\hat{f}(x)] = E[(\hat{f}(x) - E[\hat{f}(x)])^{2}]$

模型的真實誤差是兩者之和，如下式：
$E[(y - \hat{f}(x))^{2}] = Bias[\hat{f}(x)]^{2} + Var[\hat{f}(x)] + \sigma ^{2}$

如果是小訓練集，高偏差/低方差的分類器（例如，樸素貝葉斯NB）要比低偏差/高方差大分類的優勢大（例如，KNN），因為後者會過擬合。但是，隨著你訓練集的增長，模型對於原數據的預測能力就越好，偏差就會降低，此時低偏差/高方差分類器就會漸漸的表現其優勢（因為它們有較低的漸近誤差），此時高偏差分類器此時已經不足以提供准確的模型了。

當然，你也可以認為這是生成模型（混合高斯模型、樸素貝葉斯，隱馬爾科夫模型等）與判別模型（KNN、SVM、LR等）的一個區別。

在概率統計理論中, 生成模型(Generatve Model)是指能夠隨機生成觀測數據的模型，尤其是在給定某些隱含參數的條件下。它給觀測值和標註數據序列指定一個聯合概率分佈。在機器學習中，生成模型可以用來直接對數據建模（例如根據某個變量的概率密度函數進行數據採樣），也可以用來建立變量間的條件概率分佈。條件概率分佈可以由生成模型根據貝葉斯准測形成。

在機器學習領域判別模型(Discriminative Model)是一種對未知數據 $y$ 與已知數據 $x$ 之間關係進行建模的方法。判別模型是一種基於概率理論的方法。已知輸入變量 $x$ ，判別模型通過構建條件概率分佈 $P(y|x)$ 預測 $y$ 。

與生成模型不同，判別模型不考慮 $x$ 與 $y$ 間的聯合分佈。對於諸如分類和回歸問題，由於不考慮聯合概率分佈，採用判別模型可以取得更好的效果。而生成模型在刻畫複雜學習任務中的依賴關係方面則較判別模型更加靈活。大部分判別模型本身是監督學習模型，不易擴展用於非監督學習過程。實踐中，需根據應用的具體特性來選取判別模型或生成模型。

為什麼說樸素貝葉斯是高偏差低方差?
以下內容引自知乎：

首先，假設你知道訓練集和測試集的關系。簡單來講是我們要在訓練集上學習一個模型，然後拿到測試集去用，效果好不好要根據測試集的錯誤率來衡量。但很多時候，我們只能假設測試集和訓練集的是符合同一個數據分布的，但卻拿不到真正的測試數據。這時候怎麼在只看到訓練錯誤率的情況下，去衡量測試錯誤率呢？

由於訓練樣本很少（至少不足夠多），所以通過訓練集得到的模型，總不是真正正確的。（就算在訓練集上正確率100%，也不能說明它刻畫了真實的數據分布，要知道刻畫真實的數據分布才是我們的目的，而不是只刻畫訓練集的有限的數據點）。而且，實際中，訓練樣本往往還有一定的噪音誤差，所以如果太追求在訓練集上的完美而采用一個很復雜的模型，會使得模型把訓練集裡面的誤差都當成了真實的數據分布特征，從而得到錯誤的數據分布估計。這樣的話，到了真正的測試集上就錯的一塌糊塗了（這種現像叫過擬合）。但是也不能用太簡單的模型，否則在數據分布比較復雜的時候，模型就不足以刻畫數據分布了（體現為連在訓練集上的錯誤率都很高，這種現像較欠擬合）。過擬合表明采用的模型比真實的數據分布更復雜，而欠擬合表示采用的模型比真實的數據分布要簡單。

在統計學習框架下，大家刻畫模型復雜度的時候，有這麼個觀點，認為Error = Bias + Variance。這裡的Error大概可以理解為模型的預測錯誤率，是有兩部分組成的，一部分是由於模型太簡單而帶來的估計不准確的部分（Bias），另一部分是由於模型太復雜而帶來的更大的變化空間和不確定性（Variance）。

所以，這樣就容易分析樸素貝葉斯了。它簡單的假設了各個數據之間是無關的，是一個被嚴重簡化了的模型。所以，對於這樣一個簡單模型，大部分場合都會Bias部分大於Variance部分，也就是說高偏差而低方差。

在實際中，為了讓Error盡量小，我們在選擇模型的時候需要平衡Bias和Variance所占的比例，也就是平衡over-fitting和under-fitting。

偏差和方差與模型復雜度的關系使用下圖更加明了：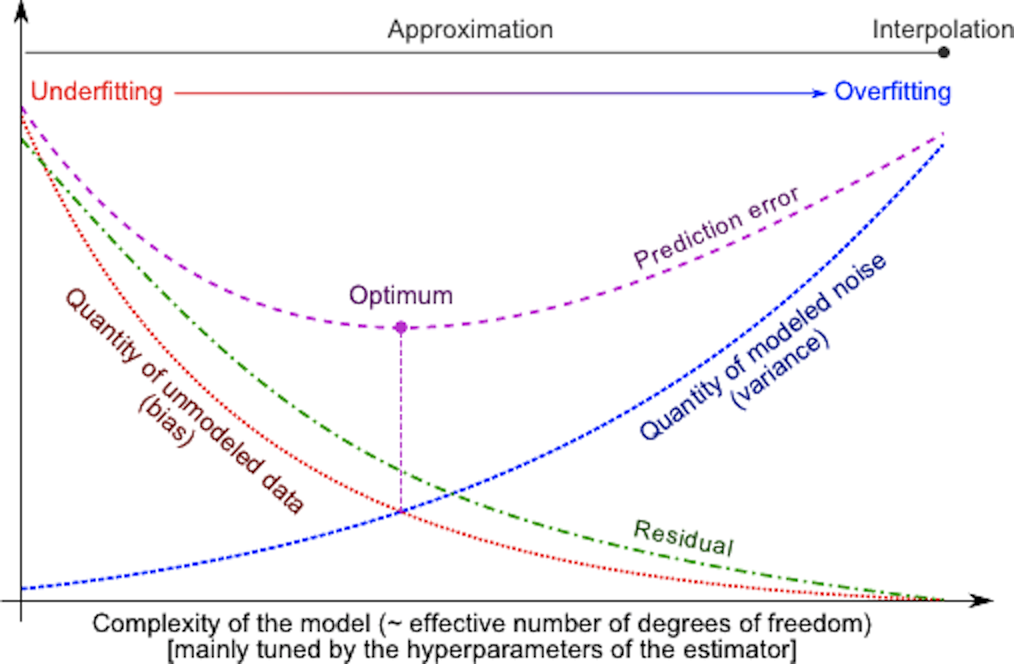

當模型復雜度上升的時候，偏差會逐漸變小，而方差會逐漸變大。

常用算法梳理

1. 樸素貝葉斯(Naive Bayes)

事件A和B同時發生的概率為在A發生的情況下發生B或者在B發生的情況下發生A。
$P(A\bigcap B) = P(A) * P(B|A) = P(B) * P(A|B)$
所以有：
$P(A|B) = \frac{P(B|A) * P(A)}{P(B)}$
對於給出的待分類項，求解在此項出現的條件下各個目標類別出現的概率，哪個最大，就認為此分類項屬於哪個類別。

工作原理

假設現在有樣本 $x = (a_{1}, a_{2}, a_{3},...a_{n})$ 這個待分類項(並認為x裡面的特徵獨立)
再假設現在有分類目標 $Y = \{ y_{1}, y_{2}, y_{3},...y_{n} \}$
那麼 $max(P(y_{1}|x), P(y_{2}|x), P(y_{3}|x),...P(y_{n}|x))$ 就是最終的分類類別
而 $P(y_{i}|x) = \frac{P(x|y_{i}) * P(y_{i})}{P(x)}$
因為 $x$ 對於每個分類目標來說都一樣，所以就是求 $max(P(x|y_{i}) * P(y_{i}))$
$P(x|y_{i}) * P(y_{i}) = P(y_{i}) * \prod _{i} (P(a_{i}|y_{i}))$
而具體的 $P(a_{i}|y_{i})$ 和 $P(y_{i})$ 都是能從訓練樣本中統計出來的。 $P(a_{i}|y_{i})$ 表示該類別下該特徵出現的概率； $P(y_{i})$ 表示全部類別中這個類別出現的概率。

工作流程

准備階段
確定特征屬性，並對每個特征屬性進行適當劃分，然後由人工對一部分待分類項進行分類，形成訓練樣本。
訓練階段
計算每個類別在訓練樣本中的出現頻率及每個特征屬性劃分對每個類別的條件概率估計
應用階段
使用分類器進行分類，輸入是分類器和待分類樣本，輸出是樣本屬於的分類類別

屬性特徵

特征為離散值時直接統計即可（表示統計概率）
特征為連續值的時候假定特征符合高斯分布: $g(x, n, u)$ ,
那麼 $P(a_{k}|y_{i}) = g(x_{k}, n_{i}, u_{i})$

Laplace校准(拉普拉斯校驗)

當某個類別下某個特征劃分沒有出現時，會有 $P(a|y) = 0$ ，就是導致分類器質量降低，所以此時引入Laplace校驗，就是對沒類別下所有劃分的計數加1。

遇到特征之間不獨立問題

參考改進的貝葉斯網絡，使用DAG來進行概率圖的描述

優缺點

優點

樸素貝葉斯模型發源於古典數學理論，有著堅實的數學基礎，以及穩定的分類效率。
對小規模的數據表現很好，能個處理多分類任務，適合增量式訓練；
對缺失數據不太敏感，算法也比較簡單，常用於文本分類。

缺點

需要計算先驗概率；
分類決策存在錯誤率；
對輸入數據的表達形式很敏感(離散、連續，值極大極小等)。

2. 邏輯回歸(Logistic Regression)

邏輯回歸(LR)是一個線性的二分類模型，主要是計算在某個樣本特征下事件發生的概率，比如根據用戶的瀏覽購買情況作為特征來計算它是否會購買這個商品，抑或是它是否會點擊這個商品。然後LR的最終值是根據一個線性和函數再通過一個sigmoid函數來求得，這個線性和函數權重與特征值的累加以及加上偏置求出來的，所以在訓練LR時也就是在訓練線性和函數的各個權重值w。
$h_{\theta}(x) = \frac{1}{1 + e^{-(\theta^{T}x + b)}}$
where
$g(z) = \frac{1}{1 + e^{-z}}$
其導數形式為：
$g'(z) = \frac{d}{dz} \frac{1}{1 + e^{-z}} \\ = \frac{1}{(1 + e^{-z})^{2}} (e^{-z}) \\ = \frac{1}{1 + e^{-z}} \cdot (1 - \frac{1}{1 + e^{-z}}) \\ = g(z)(1-g(z))$

邏輯回歸方法主要是用最大似然估計來學習的，所以單個樣本的後驗概率為：
$P(y|x;\theta ) = (h_{\theta }(x))^{y}(1-h_{\theta }(x))^{1-y}$
到整個樣本的後驗概率為：
$L(\theta ) = P(\vec{y}|X;\theta ) \\ = \prod _{i = 1}^{m}P(y^{(i)}|x^{(i)};\theta ) \\ = \prod _{i = 1}^{m}(h_{\theta }(x^{(i)}))^{y^{(i)}}(1-h_{\theta }(x^{(i)}))^{1-y^{(i)}}$
其中：
$P(y = 1|x; \theta ) = h_{\theta }(x)$
$P(y = 0|x; \theta ) = 1 - h_{\theta }(x)$
通過對數進一步化簡為：
$l(\theta ) = logL(\theta ) \\ = \sum _{i = 1}^{m}y^{(i)}logh(x^{(i)}) + (1 - y^{(i)})log(1 - h(x^{(i)}))$
其實它的損失函數(Loss Function)為 $-l(\theta )$ ，因此我們需使Loss Function最小，可採用梯度下降法得到。梯度下降法公式為：
$\frac{\partial }{\partial \theta _{j}}l(\theta ) = (y\frac{1}{g(\theta ^{T}x)}-(1-y)\frac{1}{1-g(\theta ^{T}x)})\frac{\partial }{\partial \theta _{j}}g(\theta ^{T}x) \\ = (y\frac{1}{g(\theta ^{T}x)}-(1-y)\frac{1}{1-g(\theta ^{T}x)})g(\theta ^{T}x)(1-g(\theta ^{T}x))\frac{\partial }{\partial \theta _{j}}\theta ^{T}x \\ = (y(1-g(\theta ^{T}x))-(1-y)g(\theta ^{T}x))x_{j} \\ = (y-h_{\theta }(x))x_{j}$
$\theta _{j} := \theta _{j} + \alpha (y^{(i)}-h_{\theta }(x^{(i)}))x_{j}^{(i)}$
其中α為步長，直到 $l(\theta)$ 不能再小時停止

梯度下降法的最大問題就是會陷入局部最優，並且每次在對當前樣本計算cost的時候都需要去遍歷全部樣本才能得到cost值，這樣計算速度就會慢很多（雖然在計算的時候可以轉為矩陣乘法去更新整個w值）
所以現在好多框架（mahout）中一般使用隨機梯度下降法，它在計算cost的時候只計算當前的代價，最終cost是在全部樣本迭代一遍之求和得出，還有他在更新當前的參數w的時候並不是依次遍歷樣本，而是從所有的樣本中隨機選擇一條進行計算，它方法收斂速度快（一般是使用最大迭代次數），並且還可以避免局部最優，並且還很容易並行（使用參數服務器的方式進行並行）

其他優化方法

擬牛頓法
BFGS
L-BFGS

優缺點：無需選擇學習率α，更快，但是更複雜

優缺點

優點

實現簡單；
分類時計算量非常小，速度很快，存儲資源低；
便利的觀測樣本概率分佈
多重共線性問題可以結合L2正則化來解決。

缺點

容易欠擬合，一般準確度不太高；
只能處理兩分類問題(在此基礎上衍生出來的softmax可以用於多分類)，且必須線性可分；
不能很好的處理大量多類特徵或變量；
對於非現性特徵，需要進行轉換。

3. 線性回歸(Linear Regression)

線性回歸才是真正用於回歸的，而不像logistic回歸是用於分類，其基本思想是用梯度下降法對最小二乘法形式的誤差函數進行優化，當然也可以用normal equation直接求得參數的解，結果為：
$\hat{w} = (X^{T}X)^{-1}X^{T}y$

而在LWLR（局部加權線性回歸）中，參數的計算表達式為:
$\hat{w} = (X^{T}WX)^{-1}X^{T}Wy$

因為此時優化的是：
$1.\ Fit\ \theta \ to\ minimize\ \sum _{i}w^{(i)}(y^{(i)}-\theta ^{T}x^{(i)})^{2}.$
$2.\ Output\ \theta ^{T}x.$

由此可見LWLR與LR不同，LWLR是一個非參數模型，因為每次進行回歸計算都要遍歷訓練樣本至少一次。

優缺點

優點

實現簡單，計算簡單。

缺點

不能擬合非線性數據。

羅輯回歸與線性回歸的區別

線性回歸要求變量服從正態分布，logistic回歸對變量分布沒有要求。
線性回歸要求因變量是連續性數值變量，而logistic回歸要求因變量是分類型變量。
線性回歸要求自變量和因變量呈線性關系，而logistic回歸不要求自變量和因變量呈線性關系。
logistic回歸是分析因變量取某個值的概率與自變量的關系，而線性回歸是直接分析因變量與自變量的關系。

總之, logistic回歸與線性回歸實際上有很多相同之處，最大的區別就在於他們的因變量不同，其他的基本都差不多，正是因為如此，這兩種回歸可以歸於同壹個家族，即廣義線性模型（generalized linear model）。這一家族中的模型形式基本上都差不多，不同的就是因變量不同，如果是連續的，就是多重線性回歸，如果是二項分布，就是logistic回歸。logistic回歸的因變量可以是二分類的，也可以是多分類的，但是二分類的更為常用，也更加容易解釋。所以實際中最為常用的就是二分類的logistic回歸。

4. KNN算法

KNN即最近鄰算法，其主要過程為：

計算訓練樣本和測試樣本中每個樣本點的距離（常見的距離度量有歐式距離，馬氏距離等）；
對上面所有的距離值進行排序；
選前k個最小距離的樣本；
根據這k個樣本的標簽進行投票，得到最後的分類類別。

如何選擇一個最佳的K值，這取決於數據。一般情況下，在分類時較大的K值能夠減小噪聲的影響。但會使類別之間的界限變得模糊。一個較好的K值可通過各種啟發式技術來獲取，比如，交叉驗證。另外噪聲和非相關性特征向量的存在會使K近鄰算法的准確性減小。

近鄰算法具有較強的一致性結果。隨著數據趨於無限，算法保證錯誤率不會超過貝葉斯算法錯誤率的兩倍。對於一些好的K值，K近鄰保證錯誤率不會超過貝葉斯理論誤差率。

三要素

K值的選擇；
距離的度量(常見的距離度量有歐式距離，馬氏距離等)；
分類決策規則(多數表決規則)。

K值的選擇

K值越小表明模型越複雜，更加容易過擬合；
但是K值越大，模型越簡單，如果K = N的時候就表明無論什麼點都是訓練集中類別最多的那個類。

所以一般k會取一個較小的值，然後用過交叉驗證來確定。
這裡所謂的交叉驗證就是將樣本劃分一部分出來為預測樣本，比如95%訓練，5%預測，然後K分別取1，2，3，4，5之類的，進行預測，計算最後的分類誤差，選擇誤差最小的K。

KNN的回歸

在找到最近的k個實例之後，可以計算這k個實例的平均值作為預測值。或者還可以給這k個實例添加一個權重再求平均值，這個權重與度量距離成反比（越近權重越大）。

優缺點

優點

思想簡單，理論成熟，即可以用來做分類也可以用來做回歸；
可用於非線性分類；
訓練時間複雜度為O(n)；
準確度高，對數據沒有假設，對outliers不敏感。

缺點

計算量大；
樣本不均衡問題；
需要大量的內存。

KD樹

KD樹是一個二叉樹，表示對K維空間的一個劃分，可以進行快速檢索（那KNN計算的時候不需要對全樣本進行距離的計算了）。

構造KD樹

在k維的空間上循環找子區域的中位數進行劃分的過程。
假設現在有K維空間的數據集 $T = \{x_{1}, x_{2}, x_{3}, ...x_{n}\}, x_{i } = \{a_{1}, a_{2}, a_{3},... a_{k}\}$

首先構造根節點，以坐標 $a_{1}$ 的中位數b為切分點，將根結點對應的矩形局域劃分為兩個區域，區域1中 $a_{1}$ >b，區域2中 $a_{1}$ \<b。
構造葉子節點，分別以上面兩個區域中 $a_{2}$ 的中位數作為切分點，再次將他們兩兩劃分，作為深度1的葉子節點，（如果 $a_{2}$ =中位數，則 $a_{2}$ 的實例落在切分面）
不斷重復2的操作，深度為j的葉子節點劃分的時候，索取的 $a_{i}$ 的i=j%k+1，直到兩個子區域沒有實例時停止。
KD樹的搜索
首先從根節點開始遞歸往下找到包含x的葉子節點，每一層都是找對應的 $x_{i}$
將這個葉子節點認為是當前的“近似最近點”
遞歸向上回退，如果以x圓心，以“近似最近點”為半徑的球與根節點的另一半子區域邊界相交，則說明另一半子區域中存在與x更近的點，則進入另一個子區域中查找該點並且更新”近似最近點“
重復3的步驟，直到另一子區域與球體不相交或者退回根節點
最後更新的”近似最近點“與x真正的最近點

KD樹進行KNN查找

通過KD樹的搜索找到與搜索目標最近的點，這樣KNN的搜索就可以被限制在空間的局部區域上了，可以大大增加效率。

KD樹搜索的復雜度

當實例隨機分布的時候，搜索的復雜度為log(N)，N為實例的個數，KD樹更加適用於實例數量遠大於空間維度的KNN搜索，如果實例的空間維度與實例個數差不多時，它的效率基於等於線性掃描。

5. SVM, SMO

對於樣本點 $(x_{i}, y_{i})$ 以及svm的超平面： $w^{T}x_{i} + b = 0$

函數間隔： $y_{i}(w^{T}x_{i} + b)$
幾何間隔： $\frac{y_{i}(w^{T}x_{i} + b)}{||w||}$ ,其中||w||為w的L2範數，幾何間隔不會因為參數比例的改變而改變

svm的基本想法就是求解能正確劃分訓練樣本並且其幾何間隔最大化的超平面。

線性SVM問題

先來看SVM的問題:
$\underset{w, b}{arg \max } \ \gamma \\ st. \frac{y_{i}(w^{T}x + b)}{||w||} \geq \gamma$
那麼假設 $\hat{\gamma} = \gamma * ||w||$
則將問題轉為：
$\underset{w, b}{arg \max } \ \frac{\hat{\gamma}}{||w||} \\ st. \ y_{i}(w^{T}x + b) \geq 1$
由於γ̂的成比例增減不會影響實際間距，所以這裡的取γ̂ =1，又因為 $max(\frac{1}{||w||}) = min(\frac{1}{2}*||w||^{2})$
所以最終的問題就變為了
$\underset{w, b}{arg \min} \ \frac{1}{2}*||w||^{2} \\ st. \ y_{i}(w^{T}x_{i} + b) \geq 1$
這樣就變成了一個凸的二次規劃化，可以將其轉換為拉格朗日函數，然後使用對偶算法來求解

對偶求解

引進拉格朗日乘子 $\alpha = \{\alpha _{1}, \alpha _{2}, \alpha _{3}, ...\alpha _{n}\}$ ,定義拉格朗日函數：
$L(w, b, a) = \frac{1}{2} *||w||^{2} - \sum_{i=1}^{ }N(\alpha _{i}*y_{i}(w^{T}x_{i}+b))+\sum (\alpha _{i})$
根據對偶性質原始問題就是求對偶問題的極大極小
$\underset{\alpha}{max}\underset{w,b}{min}L(w,b,\alpha)$
先求L對w,b的極小，再求對α的極大。
求 $\underset{w,b}{min}L(w,b,\alpha)$ ，也就是相當於對w,b求偏導並且另其等於0
$\bigtriangledown _{w}L(w,b,\alpha) = w - \sum_{i=1}^{ }N(\alpha _{i}y_{i}x_{i}) = 0 \\ \bigtriangledown _{w}L(w,b,\alpha) = \sum_{i=1}^{ }N(\alpha _{i}y_{i}) = 0$
代入後可得
$\underset{w,b}{min}L(w,b,\alpha) = -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}(\alpha _{i}\alpha _{j}y_{i}y_{j}(x_{i}\cdot x_{j})) + \sum_{i=1}^{N}\alpha _{i}$
求 $\underset{w,b}{min}L(w,b,\alpha)$ 對α的極大，即是對偶問題:
$\underset{\alpha}{max} - \frac{1}{2}*\sum_{i=1}^{N}\sum_{j=1}^{N}(\alpha _{i}\alpha _{j}y_{i}y_{j}(x_{i}\cdot x_{j}))+\sum_{i=1}^{N}\alpha_{i}$
$st. \ \sum_{i=1}^{ }N(\alpha_{i}y_{i}) = 0$
$\alpha\geq 0, i = 1,2,3, ... N$
將求最大轉為求最小，得到等價的式子為：
$\underset{\alpha}{min} \frac{1}{2}*\sum_{i=1}^{N}\sum_{j=1}^{N}(\alpha _{i}\alpha _{j}y_{i}y_{j}(x_{i}\cdot x_{j}))-\sum_{i=1}^{N}\alpha_{i}$
$st. \ \sum_{i=1}^{ }N(\alpha_{i}y_{i}) = 0$
$\alpha\geq 0, i = 1,2,3, ... N$
假如求解出來的α為 $\alpha^{*} = (\alpha _{1}^{*}, \alpha _{2}^{*}, \alpha _{3}^{*}, ...\alpha _{n}^{*})$
則得到最優的w,bw,b分別為
$w^{*} = \sum_{i=1}^{N}(\alpha _{i}^{*}y_{i}x_{i}) \\ b^{*} = y_{i} - \sum_{i=1}^{N}(\alpha_{i}^{*}y_{i}(x_{i}\cdot x_{j}))$
所以，最終的決策分類面為
$f(x) = sign(\sum_{i=1}^{N}(\alpha_{i}^{*}y_{i}(x_{i}\cdot x_{j})+b^{*}))$
也就是說，分類決策函數只依賴於輸入xx與訓練樣本的輸入的內積。

ps：上面介紹的是SVM的硬間距最大化，還有一種是軟間距最大化，引用了松弛變量ζ，則SVM問題變為:
$\underset{w,b}{arg \min} \ \frac{1}{2}*||w||^{2}+C\sum_{i=1}^{N}\zeta _{i}$
$st. \ y_{i}(w^{T}x_{i}+b) \geq 1 - \zeta _{i}$
$\zeta _{i} \geq 0, i = 1,2,3,...N$

其余解決是與硬間距的一致。
還有：與分離超平面最近的樣本點稱為支持向量。

損失函數

損失函數為（優化目標）:
$\sum_{i=1}^{N}[1-y(w^{T}x_{i}+b)]_{+}+\lambda ||w||^{2}$
其中 $[1-y(w^{T}x_{i}+b)]_{+}$ 稱為折頁損失函數，因為:
$[1-y(w^{T}x_{i}+b)]_{+} = \begin{Bmatrix} 0 &\ if \ 1-y_{i}(w^{T}x_{i}+b)\leq 0\\ 1-y_{i}(w^{T}x_{i}+b) &\ otherwise \end{Bmatrix}$

為什麼要引入對偶算法

對偶問題往往更加容易求解(結合拉格朗日和kkt條件)
可以很自然的引用核函數（拉格朗日表達式裡面有內積，而核函數也是通過內積進行映射的）

核函數

將輸入特征x（線性不可分）映射到高維特征R空間，可以在R空間上讓SVM進行線性可以變，這就是核函數的作用

多項式核函數: $K(x,z) = (x*z+1)^{p}$
高斯核函數: $K(x,z) = exp(\frac{-(x-z)^{2}}{\sigma ^{2}})$
字符串核函數：貌似用於字符串處理等

對於核函數的選擇也是有技巧的(libsvm中自帶了四種核函數：線性核、多項式核、RBF核以及Sigmoid核)：

如果樣本數量小於特征數，那麼就沒必要選擇非線性核，簡單的使用線性核就可以了；
如果樣本數量大於特征數目，這時可以使用非線性核，將樣本映射到更高維度，一般可以得到更好的結果；
如果樣本數目和特征數目相等，該情況可以使用非線性核，原理和第二種一樣。
對於第一種情況，也可以先對數據進行降維，然後使用非線性核，這也是一種方法。

優缺點

優點

可用於線性、非線性分類，也可以用於回歸；
低泛化誤差；
容易解釋；
計算複雜度較低；
使用核函數可以向高維空間進行映射，解決高維問題，即大型特徵空間；
使用核函數可以解決非線性的分類；
分類思想很簡單，就是將樣本與決策面的間隔最大化；
分類效果較好；
無需依賴整個數據。

缺點

對參數和核函數的選擇比較敏感，對非線性問題沒有通用解決方案，有時候很難找到一個合適的核函數；
原始的SVM只比較擅長處理二分類問題，但是可以使用間接的方法來做；
對大規模數據訓練比較困難；
對確實數據敏感。

SMO

SMO是用於快速求解SVM的。
它選擇凸二次規劃的兩個變量，其他的變量保持不變，然後根據這兩個變量構建一個二次規劃問題，這個二次規劃關於這兩個變量解會更加的接近原始二次規劃的解，通過這樣的子問題劃分可以大大增加整個算法的計算速度，關於這兩個變量：

其中一個是嚴重違反KKT條件的一個變量
另一個變量是根據自由約束確定，好像是求剩余變量的最大化來確定的。

SVM多分類問題

直接法
直接在目標函數上進行修改，將多個分類面的參數求解合並到一個最優化問題中，通過求解該優化就可以實現多分類（計算復雜度很高，實現起來較為困難）。
間接法
一對多
其中某個類為一類，其余n-1個類為另一個類，比如A,B,C,D四個類，第一次A為一個類，{B,C,D}為一個類訓練一個分類器，第二次B為一個類,{A,C,D}為另一個類,按這方式共需要訓練4個分類器，最後在測試的時候將測試樣本經過這4個分類器 $f_{1}(x), f_{2}(x), f_{3}(x) \and\ f_{4}(x)$ ,取其最大值為分類器(這種方式由於是1對M分類，會存在偏置，很不實用)
一對一(libsvm實現的方式)
任意兩個類都訓練一個分類器，那麼n個類就需要n(n-1)/2個svm分類器。
還是以A,B,C,D為例,那麼需要{A,B},{A,C},{A,D},{B,C},{B,D},{C,D}為目標共6個分類器，然後在預測的將測試樣本通過這6個分類器之後進行投票選擇最終結果。（這種方法雖好，但是需要n(n-1)/2個分類器代價太大，不過有好像使用循環圖來進行改進）。

6. 決策樹(Decision Tree)

決策樹是一顆依托決策而建立起來的樹。

ID3

首先是針對當前的集合，計算每個特征的信息增益
然後選擇信息增益最大的特征作為當前節點的決策決策特征
根據特征不同的類別劃分到不同的子節點（比如年齡特征有青年，中年，老年，則劃分到3顆子樹）
然後繼續對子節點進行遞歸，直到所有特征都被劃分

$S(C,a_{i}) = -\sum_{i}^{ }(p_{i}*log(p_{i}))$
一個屬性中某個類別的熵 $p_{i}=p(y_{i}|a_{i}),\ p_{i}$ 表示 $a_{i}$ 情況下發生 $y_{i}$ 的概率，也即是統計概率。
$S(C,A) = \sum_{i}^{ }(p(A = a_{i})*S(a_{i}))$
整個屬性的熵，為各個類別的比例與各自熵的加權求和。
Gain(C,A)=S(C)−S(C,A)
增益表示分類目標的熵減去當前屬性的熵，增益越大，分類能力越強
(這裡前者叫做經驗熵，表示數據集分類C的不確定性，後者就是經驗條件熵，表示在給定A的條件下對數據集分類C的不確定性，兩者相減叫做互信息，決策樹的增益等價於互信息)。

關於損失函數
設樹的葉子節點個數為T，t為其中一個葉子節點，該葉子節點有 $N_{t}$ 個樣本，其中k類的樣本有 $N_{tk}$ 個，H(t)為葉子節點上的經驗熵，則損失函數定義為
$C_{t}(T) = \sum (N_{t}*H(t))+\lambda |T|$
其中
$H(t) = \sum (\frac{N_{tk}}{N_{t}}*log(\frac{N_{tk}}{N_{t}}))$
代入可以得到
$C_{t}(T) = \sum (\sum (N_{tk}*log\frac{N_{tk}}{N_{t}})) + \lambda |T|$
λ|T|為正則化項，λ是用於調節比率
決策樹的生成只考慮了信息增益

C4.5

它是ID3的一個改進算法，使用信息增益率來進行屬性的選擇
$splitInformation(S,A) = -\sum_{i}^{ }(\frac{|S_{i}|}{|S|}*log \ 2 (\frac{|S_{i}|}{|S|}))$
$GainRation(S,A) =\frac{Gain(S,A)}{splitInformation(S,A)}$

優缺點：
准確率高，但是子構造樹的過程中需要進行多次的掃描和排序，所以它的運算效率較低

Cart

分類回歸樹(Classification And Regression Tree)是一個決策二叉樹，在通過遞歸的方式建立，每個節點在分裂的時候都是希望通過最好的方式將剩余的樣本劃分成兩類，這裡的分類指標：

分類樹：基尼指數最小化(gini_index)
回歸樹：平方誤差最小化

分類樹：

首先是根據當前特征計算他們的基尼增益
選擇基尼增益最小的特征作為劃分特征
從該特征中查找基尼指數最小的分類類別作為最優劃分點
將當前樣本劃分成兩類，一類是劃分特征的類別等於最優劃分點，另一類就是不等於
針對這兩類遞歸進行上述的劃分工作，直達所有葉子指向同一樣本目標或者葉子個數小於一定的閾值

gini用來度量分布不均勻性（或者說不純），總體的類別越雜亂，gini指數就越大（跟熵的概念很相似）
$gini(a_{i}) = 1 - \sum_{i}^{ }(p_{i}^{2})$
$p_{i}$ 當前數據集中第i類樣本的比例
gini越小，表示樣本分布越均勻（0的時候就表示只有一類了），越大越不均勻
基尼增益
$gini\_gain = \sum_{i}^{ }(\frac{N_{i}}{N*gini(a_{i})})$
表示當前屬性的一個混亂， $\frac{N_{i}}{N}$ 表示當前類別占所有類別的概率。
最終Cart選擇GiniGain最小的特征作為劃分特征。

回歸樹：

回歸樹是以平方誤差最小化的准則劃分為兩塊區域

遍歷特征計算最優的劃分點s，
使其最小化的平方誤差是： $min\{min(R1.sigma((y_{i}-c_{1})^{2}))+min(R2.sigma((y_{i}-c_{2})^{2}))\}$
計算根據s劃分到左側和右側子樹的目標值與預測值之差的平方和最小，這裡的預測值是兩個子樹上輸入 $x_{i}$ 樣本對應 $y_{i}$ 的均值
找到最小的劃分特征j以及其最優的劃分點s,根據特征j以及劃分點s將現有的樣本劃分為兩個區域，一個是在特征j上小於等於s，另一個在在特征j上大於s
$R1(j) = {x|x(j)\leq s}$
$R2(j) = {x|x(j)\geq s}$
進入兩個子區域按上述方法繼續劃分，直到到達停止條件。

這裡面的最小化我記得可以使用最小二乘法來求

關於剪枝：用獨立的驗證數據集對訓練集生長的樹進行剪枝（事後剪枝）。

停止條件

直到每個葉子節點都只有一種類型的記錄時停止，（這種方式很容易過擬合）
另一種時當葉子節點的記錄樹小於一定的閾值或者節點的信息增益小於一定的閾值時停止

關於特征與目標值

特征離散目標值離散：可以使用ID3，cart
特征連續目標值離散：將連續的特征離散化可以使用ID3，cart
特征離散目標值連續

決策樹的分類與回歸

分類樹
輸出葉子節點中所屬類別最多的那一類
回歸樹
輸出葉子節點中各個樣本值的平均值

理想的決策樹

葉子節點數盡量少
葉子節點的深度盡量小(太深可能會過擬合)

解決決策樹的過擬合

剪枝
前置剪枝：在分裂節點的時候設計比較苛刻的條件，如不滿足則直接停止分裂（這樣干決策樹無法到最優，也無法得到比較好的效果）
後置剪枝：在樹建立完之後，用單個節點代替子樹，節點的分類采用子樹中主要的分類（這種方法比較浪費前面的建立過程）
交叉驗證
隨機森林

優缺點

優點

計算量簡單，易於理解，可解釋性強；
比較適合處理有缺失屬性值的樣本；
能夠處理不相關的特征；
在相對短的時間內能夠對大型數據源做出可行且效果良好的結果。

缺點

單顆決策樹分類能力弱，並且對連續值變量難以處理；
容易過擬合（後續出現了隨機森林，減小了過擬合現像）；
忽略了數據之間的相關性；
對於那些各類別樣本數量不一致的數據，在決策樹當中，信息增益的結果偏向於那些具有更多數值的特徵(只要是用了信息增益，都有這個缺點，如RF)。

7. 隨機森林(Random Forest)

隨機森林是有很多隨機得決策樹構成，它們之間沒有關聯。得到RF以後，在預測時分別對每一個決策樹進行判斷，最後使用Bagging的思想進行結果的輸出（也就是投票的思想）。
一般很多的決策樹算法都一個重要的步驟——剪枝，但隨機森林不這樣做，由於之前的兩個隨機采樣的過程保證了隨機性，所以就算不剪枝，也不會出現over-fitting。按這種算法得到的隨機森林中的每一棵都是很弱的，但是大家組合起來就很厲害了。可以這樣比喻隨機森林算法：每一棵決策樹就是一個精通於某一個窄領域的專家（因為我們從M個feature中選擇m讓每一棵決策樹進行學習），這樣在隨機森林中就有了很多個精通不同領域的專家，對一個新的問題（新的輸入數據），可以用不同的角度去看待它，最終由各個專家，投票得到結果。

學習過程

現在有N個訓練樣本，每個樣本的特征為M個，需要建K顆樹。
從N個訓練樣本中有放回的取N個樣本作為一組訓練集（其余未取到的樣本作為預測分類，評估其誤差）,這樣使得在訓練的時候，每一棵樹的輸入樣本都不是全部的樣本，使得相對不容易出現over-fitting。
從M個特征中取m個特征左右子集特征(m<<M)。
對采樣的數據使用完全分裂的方式來建立決策樹，這樣的決策樹每個節點要麼無法分裂，要麼所有的樣本都指向同一個分類。
重復2的過程K次，即可建立森林。

預測過程

將預測樣本輸入到K顆樹分別進行預測
如果是分類問題，直接使用投票的方式選擇分類頻次最高的類別
如果是回歸問題，使用分類之後的均值作為結果

參數問題

這裡的一般取m=sqrt(M)
關於樹的個數K，一般都需要成百上千，但是也有具體的樣本有關（比如特征數量）
樹的最大深度，（太深可能可能導致過擬合？？）
節點上的最小樣本數、最小信息增益

泛化誤差估計

使用oob（out-of-bag）進行泛化誤差的估計，將各個樹的未采樣樣本作為預測樣本（大約有36.8%），使用已經建立好的森林對各個預測樣本進行預測，預測完之後最後統計誤分得個數占總預測樣本的比率作為RF的oob誤分率。

學習算法

ID3算法：處理離散值的量
C45算法：處理連續值的量
Cart算法：離散和連續兩者都合適？

關於CART

Cart可以通過特征的選擇迭代建立一顆分類樹，使得每次的分類平面能最好的將剩余數據分為兩類
$gini = 1 - \sum (p_{i}^{2})$ ，表示每個類別出現的概率和與1的差值。
分類問題：argmax(Gini−GiniLeft−GiniRight)
回歸問題：argmax(Var−VarLeft−VarRight)
查找最佳特征f已經最佳屬性閾值th 小於th的在左邊，大於th的在右邊子樹

優缺點

能夠處理大量特征的分類，並且還不用做特征選擇；
在訓練完成之後能給出哪些feature的比較重要；
訓練速度很快；
很容易並行；
實現相對來說較為簡單。

8. Bagging, Boosting與Adaboost

Bagging算法描述

模型生成
令n為訓練數據的實例數量
對於t次循環中的每一次
    從訓練數據中采樣n個實例
    將學習應用於所采樣本
    保存結果模型
分類
對於t個模型的每一個
    使用模型對實例進行預測
返回被預測次數最多的一個

bagging：bootstrap aggregating的縮寫。讓該學習算法訓練多輪，每輪的訓練集由從初始的訓練集中隨機取出的n個訓練樣本組成，某個初始訓練樣本在某輪訓練集中可以出現多次或根本不出現，訓練之後可得到一個預測函數序列
$h_{1}, h_{2}, h_{3}, ...h_{n},$
最終的預測函數H對分類問題采用投票方式，對回歸問題采用簡單平均方法對新示例進行判別。

[訓練R個分類器f_i，分類器之間其他相同就是參數不同。其中f_i是通過從訓練集合中(N篇文檔)隨機取(取後放回)N次文檔構成的訓練集合訓練得到的。對於新文檔d，用這R個分類器去分類，得到的最多的那個類別作為d的最終類別。]

Boosting算法描述

模型生成
賦予每個訓練實例相同的權值
t次循環中的每一次：
    將學習算法應用於加了權的數據集上並保存結果模型
    計算模型在加了權的數據上的誤差e並保存這個誤差
    結果e等於0或者大於等於0.5：
        終止模型
    對於數據集中的每個實例：
        如果模型將實例正確分類
            將實例的權值乘以e/(1-e)
    將所有的實例權重進行正常化
分類
賦予所有類權重為0
對於t（或小於t）個模型中的每一個：
    給模型預測的類加權 -log(e/(1-e))
返回權重最高的類

boosting: 其中主要的是AdaBoost（Adaptive boosting，自適應boosting）。初始化時對每一個訓練例賦相等的權重1／N，然後用該學算法對訓練集訓練t輪，每次訓練後，對訓練失敗的訓練例賦以較大的權重，也就是讓學習算法在後續的學習中集中對比較難的訓練例進行學習，從而得到一個預測函數序列h1,⋯,hmh1,⋯,hm , 其中h_i也有一定的權重，預測效果好的預測函數權重較大，反之較小。最終的預測函數H對分類問題采用有權重的投票方式，對回歸問題采用加權平均的方法對新示例進行判別。

提升算法理想狀態是這些模型對於其他模型來說是一個補充，每個模型是這個領域的一個專家，而其他模型在這部分卻不能表現很好，就像執行官一樣要尋覓那些技能和經驗互補的顧問，而不是重復的。這與裝袋算法有所區分。

Adaboost算法描述

模型生成
訓練數據中的每個樣本，並賦予一個權重，構成權重向量D，初始值為1/N
t次循環中的每一次：
    在訓練數據上訓練弱分類器並計算分類器的錯誤率e
    如果e等於0或者大於等於用戶指定的閾值：
        終止模型，break
    重新調整每個樣本的權重，其中alpha=0.5*ln((1-e)/e)
    對權重向量D進行更新，正確分類的樣本的權重降低而錯誤分類的樣本權重值升高
    對於數據集中的每個樣例：
        如果某個樣本正確分類：
            權重改為D^(t+1)_i = D^(t)_i * e^(-a)/Sum(D)
        如果某個樣本錯誤分類：
            權重改為D^(t+1)_i = D^(t)_i * e^(a)/Sum(D)
分類
賦予所有類權重為0
對於t（或小於t）個模型（基分類器）中的每一個：
    給模型預測的類加權 -log(e/(1-e))
返回權重最高的類

（類似Bagging方法，但是訓練是串行進行的，第k個分類器訓練時關注對前k-1分類器中錯分的文檔，即不是隨機取，而是加大取這些文檔的概率。)

優缺點

優點

低泛化誤差；
容易實現，分類準確率較高，沒有太多參數可以調。

缺點

對outliers比較敏感。

9. Gradient Boosting

GBDT的精髓在於訓練的時候都是以上一顆樹的殘差為目標，這個殘差就是上一個樹的預測值與真實值的差值。

Gradient boosting（又叫Mart, Treenet)：Boosting是一種思想，Gradient Boosting是一種實現Boosting的方法，它主要的思想是，每一次建立模型是在之前建立模型損失函數的梯度下降方向。損失函數(loss function)描述的是模型的不靠譜程度，損失函數越大，則說明模型越容易出錯。如果我們的模型能夠讓損失函數持續的下降，則說明我們的模型在不停的改進，而最好的方式就是讓損失函數在其梯度（Gradient)的方向上下降。
Boosting的好處就是每一步的參加就是變相了增加了分錯instance的權重，而對已經對的instance趨向於0，這樣後面的樹就可以更加關注錯分的instance的訓練了

Shrinkage

Shrinkage認為，每次走一小步逐步逼近的結果要比每次邁一大步逼近結果更加容易避免過擬合。
$y(1 \sim i) = y(1 \sim i - 1) + step * y_{i}$

就像我們做互聯網，總是先解決60%用戶的需求湊合著，再解決35%用戶的需求，最後才關注那5%人的需求，這樣就能逐漸把產品做好。

調參

樹的個數 100~10000
葉子的深度 3~8
學習速率 0.01~1
葉子上最大節點樹 20
訓練采樣比例 0.5~1
訓練特征采樣比例 sqrt(num)

優缺點

優點

精度高；
能處理非線性數據；
能處理多特征類型；
適合低維稠密數據。

缺點

並行麻煩（因為上下兩顆樹有聯系）；
多分類的時候復雜度很大。

10. 人工神經網絡(Neural Networks)

優點

分類的準確度高；
並行分佈處理能力強，分佈存儲及學習能力強；
對噪聲神經有較強的魯棒性和容錯能力，能充分逼近複雜的非線性關係；
具備聯想記憶功能。

缺點

需要大量的參數，如網絡拓撲結構、權值和閾值的初始值；
不能觀察之間的學習過程，輸出結果難以解釋，會影響到結果的可信度和可接受程度；
學習時間過長，甚至可能達不到學習的目的。

11. K-Means聚類

k-Means算法是一種聚類算法，它是一種無監督學習算法，目的是將相似的對像歸到同一個蔟中。蔟內的對像越相似，聚類的效果就越好。聚類和分類最大的不同在於，分類的目標事先已知，而聚類則不一樣。其產生的結果和分類相同，而只是類別沒有預先定義。

算法原理

設計的目的：使各個樣本與所在類均值的誤差平方和達到最小（這也是評價K-means算法最後聚類效果的評價標准）
$SSE = \sum_{i=1}^{k}\sum_{x\in C_{i}}^{ }||x-\mu _{i}||^{2}$

創建k個點作為K個簇的起始質心（經常隨機選擇）
當任意一個點的蔟分配結果發生變化時（初始化為True）
對數據集中的每個數據點，重新分配質心
    對每個質心
        計算質心到數據點之間的距離
    將數據點分配到距其最近的蔟
對每個蔟，計算蔟中所有點的均值並將均值作為新的質心

優缺點

優點

算法簡單，容易實現；
對處理大數據集，該算法是相對可伸縮的和高效率的，因為它的復雜度大約是O(nkt)，其中n是所有對像的數目，k是簇的數目,t是迭代的次數。通常k<<n。這個算法通常局部收斂；
算法嘗試找出使平方誤差函數值最小的k個劃分。當簇是密集的、球狀或團狀的，且簇與簇之間區別明顯時，聚類效果較好。

缺點

對數據類型要求較高，適合數值型數據；
可能收斂到局部最小值，在大規模數據上收斂較慢；
K值比較難以選取；
對初值的簇心值敏感，對於不同的初始值，可能會導致不同的聚類結果，不能保證K-Means算法收斂於全局最優解；
針對此問題，在K-Means的基礎上提出了二分K-means算法。該算法首先將所有點看做是一個簇，然後一分為二，找到最小SSE的聚類質心。接著選擇其中一個簇繼續一分為二，此處哪一個簇需要根據劃分後的SSE值來判斷。
不適合於發現非凸面形狀的簇，或者大小差別很大的簇；
對於”噪聲”和孤立點數據敏感，少量的該類數據能夠對平均值產生極大影響；
結果不穩定(受輸入順序影響)；
時間複雜度高O(nkt)，其中n是對象總數，k是簇數，t是迭代次數。

討論

K-Means算法K值如何選擇？
《大數據》中提到：給定一個合適的類簇指標，比如平均半徑或直徑，只要我們假設的類簇的數目等於或者高於真實的類簇的數目時，該指標上升會很緩慢，而一旦試圖得到少於真實數目的類簇時，該指標會急劇上升。
1) 簇的直徑是指簇內任意兩點之間的最大距離。
2) 簇的半徑是指簇內所有點到簇中心距離的最大值。
如何優化K-Means算法搜索的時間復雜度？
可以使用K-D樹來縮短最近鄰的搜索時間（NN算法都可以使用K-D樹來優化時間復雜度）。
如何確定K個簇的初始質心？
1) 選擇批次距離盡可能遠的K個點
首先隨機選擇一個點作為第一個初始類簇中心點，然後選擇距離該點最遠的那個點作為第二個初始類簇中心點，然後再選擇距離前兩個點的最近距離最大的點作為第三個初始類簇的中心點，以此類推，直至選出K個初始類簇中心點。
2) 選用層次聚類或者Canopy算法進行初始聚類，然後利用這些類簇的中心點作為KMeans算法初始類簇中心點。

聚類擴展：密度聚類、層次聚類。

12. EM

EM用於隱含變量的概率模型的極大似然估計，它一般分為兩步：
第一步求期望(E)，選取一組參數，求出在該參數下隱含變量的條件概率值；
第二步求極大(M)，結合E步求出的隱含變量條件概率，求出似然函數下界函數（本質上是某個期望函數）的最大值。
重複上面2步直至收斂。

如果概率模型的變量都是觀測變量，那麼給定數據之後就可以直接使用極大似然法或者貝葉斯估計模型參數。
但是當模型含有隱含變量的時候就不能簡單的用這些方法來估計，EM就是一種含有隱含變量的概率模型參數的極大似然估計法。
應用到的地方：混合高斯模型、混合樸素貝葉斯模型、因子分析模型。

(E Step) For each i, set
$Q_{i}(z^{(i)}) := p(z^{(i)}|x^{(i)}; \theta ).$
(M Step) set
$\theta := arg \ \underset{\theta}{max} \sum_{i}^{ }\sum_{z^{(i)}}^{ }Q_{i}(z^{(i)})log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}.$
M步公式中下界函數的推導過程：
$\sum_{i}^{ }log \ p(x^{(i)};\theta) =\sum_{i}^{ }log \sum_{z^{(i)}}^{ } p(x^{(i)},z^{(i)};\theta) \ (1)\\ =\sum_{i}^{ } \log \sum_{z^{(i)}}^{ } Q_{i}(z^{(i)}) \frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})} \ (2)\\ \\\geq \sum_{i}^{ } \sum_{z^{(i)}}^{ } Q_{i}(z^{(i)}) \frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})} \ (3)$
EM算法一個常見的例子就是GMM模型，每個樣本都有可能由k個高斯產生，只不過由每個高斯產生的概率不同而已，因此每個樣本都有對應的高斯分布（k個中的某一個），此時的隱含變量就是每個樣本對應的某個高斯分布。
GMM的E步公式如下（計算每個樣本對應每個高斯的概率）：
(E Step) For each i, j, set
$w_{j}^{(i)} := p(z^{(i)} = j|x^{(i)}; \phi , \mu ,\Sigma )$
更具體的計算公式為：
$p(z^{(i)} =j|x^{(i)};\phi ,\mu ,\Sigma )=\frac{p(x^{(i)}|z^{(i)}=j; \mu ,\Sigma )p(z^{(i)}=j;\phi )}{\sum_{l=1}^{k}p(x^{(i)}|z^{(i)}=l;\mu ,\Sigma )p(z^{(i)}=l;\phi )}$
M步公式如下(計算每個高斯的比重，均值，方差這3個參數)：
(M Step) Update the parameters:
$\phi _{j} := \frac{1}{m}\sum_{i=1}^{m}w_{j}^{(i)}$
$\mu _{i} :=\frac{\sum_{i=1}^{m}w_{j}^{(i)}x^{(i)}}{\sum_{i=1}^{m}w_{j}^{(i)}}$
$\Sigma _{j} := \frac{\sum_{i=1}^{m}w_{j}^{(i)}(x^{(i)}-\mu _{j})(x^{(i)}-\mu _{j})^{T}}{\sum_{i=1}^{m}w_{j}^{(i)}}$
關於EM算法可以參考Ng的CS229課程資料或者斯坦福機器學習公開課
另外，參考另一篇文章——從最大似然到EM算法淺解

13. Apriori與FP Growth

Apriori

Apriori是關聯分析中比較早的一種方法，主要用來挖掘那些頻繁項集合。其思想是：

如果一個項目集合不是頻繁集合，那麼任何包含它的項目集合也一定不是頻繁集合；
如果一個項目集合是頻繁集合，那麼它的任何非空子集也是頻繁集合。
Aprioir需要掃描項目表多遍，從一個項目開始掃描，舍去掉那些不是頻繁的項目，得到的集合稱為L，然後對L中的每個元素進行自組合，生成比上次掃描多一個項目的集合，該集合稱為C，接著又掃描去掉那些非頻繁的項目，重復…

FP Growth

FP Growth是一種比Apriori更高效的頻繁項挖掘方法，它只需要掃描項目表2次。其中第1次掃描獲得當個項目的頻率，去掉不符合支持度要求的項，並對剩下的項排序。第2遍掃描是建立一顆FP-Tree(frequent-patten tree)。

14. 凸優化

在機器學習中往往是最終要求解某個函數的最優值，但是一般情況下，任意一個函數的最優值求解比較困難，但是對於凸函數來說就可以有效的求解出全局最優值。

凸集

一個集合C是，當前僅當任意x,y屬於C且0≦Θ≦1，都有Θ∗x+(1−Θ)∗yΘ∗x+(1−Θ)∗y屬於C。
用通俗的話來說C集合線段上的任意兩點也在C集合中

凸函數

一個函數f其定義域(D(f))是凸集，並且對任意x,y屬於D(f)和0≦Θ≦1都有
f(Θ∗x+(1−Θ)∗y)≦Θ∗f(x)+(1−Θ)∗f(y)

用通俗的話來說就是曲線上任意兩點的割線都在曲線的上方。

常見的凸函數有：

指數函數f(x) = a^x; a > 1
負對數函數−logax
開口向上的二次函數等

凸函數的判定：

如果f是一階可導，對於任意數據域內的x,y滿足 $f(y) \geq f(x) +{f}'(x)(y-x)$
如果f是二階可導，

凸優化應用舉例

SVM：其中由max|w|轉向 $min(\frac{1}{2}*|w|^{2})$
最小二乘法？
LR的損失函數 $\sum (y_{i}*log(h_{w}(x_{i}))+(1-y_{i})*(log(1-h_{w}(x_{i}))))$

15. Regularization

數值上更容易求解；
特征數目太大時更穩定；
控制模型的復雜度，光滑性。復雜性越小且越光滑的目標函數泛化能力越強。而加入規則項能使目標函數復雜度減小，且更光滑。
減小參數空間；參數空間越小，復雜度越低。
系數越小，模型越簡單，而模型越簡單則泛化能力越強（Ng宏觀上給出的解釋）。
可以看成是權值的高斯先驗。

16. 異常檢測

可以估計樣本的密度函數，對於新樣本直接計算其密度，如果密度值小於某一閾值，則表示該樣本異常。而密度函數一般采用多維的高斯分布。如果樣本有n維，則每一維的特征都可以看作是符合高斯分布的，即使這些特征可視化出來不太符合高斯分布，也可以對該特征進行數學轉換讓其看起來像高斯分布，比如說x=log(x+c), x=x^(1/c)等。異常檢測的算法流程如下：
Anomaly detection algorithm

Choose features $x_{i}$ that you think might be indicative of anomalous examples.
Fit parameters $\mu _{1}, \mu _{2}, ...\mu _{n}, \sigma _{1}^{2}, \sigma _{2}^{2}, ... \sigma _{n}^{2}$
$\mu _{j} = \frac{1}{m}\sum_{i=1}^{m}x_{j}^{(i)}$
$\sigma _{j}^{2} = \frac{1}{m}\sum_{i=1}^{m}(x_{j}^{(i)}-\mu _{j})^{2}$
Given new example x, compute p(x):
$p(x)=\prod_{j=1}^{n}p(x_{j};\mu _{j,\sigma _{j}^{2}}) = \prod_{j=1}^{n}\frac{1}{\sqrt{2\pi }\sigma _{j}}exp(-\frac{(x_{j}-\mu _{j})^{2}}{2\sigma _{j}^{2}})$
Anomaly if p(x) < ε

其中的ε也是通過交叉驗證得到的，也就是說在進行異常檢測時，前面的p(x)的學習是用的無監督，後面的參數ε學習是用的有監督。那麼為什麼不全部使用普通有監督的方法來學習呢（即把它看做是一個普通的二分類問題）？主要是因為在異常檢測中，異常的樣本數量非常少而正常樣本數量非常多，因此不足以學習到好的異常行為模型的參數，因為後面新來的異常樣本可能完全是與訓練樣本中的模式不同。

另外，上面是將特征的每一維看成是相互獨立的高斯分布，其實這樣的近似並不是最好的，但是它的計算量較小，因此也常被使用。更好的方法應該是將特征擬合成多維高斯分布，這時有特征之間的相關性，但隨之計算量會變復雜，且樣本的協方差矩陣還可能出現不可逆的情況（主要在樣本數比特征數小，或者樣本特征維數之間有線性關系時）。

上面的內容可以參考Ng的斯坦福機器學習公開課

17. 算法選擇參考

之前翻譯過一些國外的文章，有一篇文章中給出了一個簡單的算法選擇技巧：

首當其衝應該選擇的就是邏輯回歸，如果它的效果不怎麼樣，那麼可以將它的結果作為基准來參考，在基礎上與其他算法進行比較；
然後試試決策樹（隨機森林）看看是否可以大幅度提升你的模型性能。即便最後你並沒有把它當做為最終模型，你也可以使用隨機森林來移除噪聲變量，做特征選擇；
如果特征的數量和觀測樣本特別多，那麼當資源和時間充足時（這個前提很重要），使用SVM不失為一種選擇。

通常情況下：【GBDT>=SVM>=RF>=Adaboost>=Other…】，現在深度學習很熱門，很多領域都用到，它是以神經網絡為基礎的，目前我自己也在學習，只是理論知識不是很厚實，理解的不夠深，這裡就不做介紹了。

算法固然重要，但好的數據卻要優於好的算法，設計優良特征是大有裨益的。假如你有一個超大數據集，那麼無論你使用哪種算法可能對分類性能都沒太大影響（此時就可以根據速度和易用性來進行抉擇）。

Reference: